

【第28回】データマイニング・夜話
(その十:子供の頃わくわくした事)
コラムTOPへ戻る

|
|
 |
|
【第28回】データマイニング・夜話 (その十:子供の頃わくわくした事) コラムTOPへ戻る |
|
| 前回はもっとも一般的に知られているニューロ(ニューラルネットワーク)の説明をしました。しかし、ニューロにはまだまだ幾つもの種類があります。今回はその一つであるSOMについて説明をしましょう。 SOMとは、Self Organizing Mapと言います。日本語では自己組織化法と呼ばれています。この手法はフィンランドのKohonen(コホーネン)教授が考案したので、別名コホーネンマップとも言われてる有 名なものです。その特徴はといいますと、似たもの同士を自動的に集める機能があります。 似たもののグループを作るとどういう良い事があるのでしょうか。それは、似た属性を持っているものは、その挙動、正確も似ている、ということが言える(と想定される)からです。たとえば人相見のことを考えてください。目のきつい表情の人は性格もきついとか、耳たぶが大きい人は長生きしそうだとか、お金がたまるとかいい ますね。これは、その人がそうである、と言っているわけではなく、過去に同じような顔立ちをした人にはそういうことが多く起ったという(どれほど確かかは保証はしませんが)実績に基づいている判断(だそう)です。 しかし似ているというのはどういう基準で決めるのでしょうか?こ の基準がなかなかの曲者です。一般的に言って似たものを集めるときに必要なのは、似たものを測定する尺度です。例えば、ここに国 籍の異なる人間の男女とチンパンジーのオス、メスがいたとしましょう。これを二つのグループに分けるとしたらどうするでしょうか? 大抵の人は、ヒトとチンパンジーの二つのグループに分けるでしょ う。それは、人間同士だと、たとえ国籍が異なっても意思を通じ合 えることはできますが、チンパンジーのとはそうはいかないからでしょう。つまり、この場合は、生物学的な(種族)類似度で分けたということになります。 しかし、DNAの観点から分類してみると違った結果になります。というのは、ヒトの場合、合計46本の染色体を持っていますが、その内 には二本の性染色体があります。女性には、X-Xのペアがあり、男性には、X-Yのペアがあります。つまり、男女は46本の染色体のうち1本が完全に異なっている訳ですから、男女の差は単純に計算すると 、1/46 = 0.022 あります。つまり、ヒトの男女の類似度は97.8%なのです。方や、ヒトと同性のチンパンジーとは98.4パーセントまで共通項があるとも言われています。(もっとも最近の理化学研究所の研究によるともっと差があるとも言われていますが。。。)そうすると、同性のヒトとチンパンジーの方が、ヒトの男女の差より小さいといえそうです。即ち、人間にとっては『親しきもの、汝の名はチンパンジー』だったのです。 さて、予め分類指標(たとえば、出身地、年代)があればそれで似たものを分類することは可能ですが、そうでない場合は、この例のように、何らかの形でその差を測定できなければなりません。今回 紹介しますSOMという手法は、分類指標が無いときに類似度(別名、距離といいます)をベースにして自動的に分類する手法なのです。 一つ例を使ってその方法を説明しましょう。日本には約一億人がいますが、日本全国を人口が大体等しくなるように、十個のブロックに分割することを考えてみましょう。十個のブロックに分ける訳ですから、一ブロック当たり、千万人いる勘定となります。 SOMでは次のようなプロセス(手順)でこの課題を解きます。まず、十個の点を想像してください。点というのがイメージしにくければ 、ボールでも何でもいいですから考えて下さい。この十個の点をどこでもいいから置きます。(たとえば、平家物語の悲話の一つ、俊寛が流された鬼界ヶ島に置きましょうか。)(この十個の点を代表点と呼びます。) 次に、全国の一億人のうち誰か一人を選びます。(この選ばれた人をサンプル点と呼びます。)札幌の人だとしましょう。この札幌の人と十個のボールとの地理的距離を計算します。大体2500Kmぐらい でしょうか。ボールは全て鬼界ヶ島にあるわけですから、その間の差といっても僅かですが、それでも札幌に一番近いボールが一個あるはずですね。(このボールのことを勝者と呼びます。)このボールを札幌の方向に距離の 1/10 だけ(250Km)移動させます。そうすると海の中に落ちてしまいそうですが、紙の地図の上で移動させたと考えて下さい。 次にまた任意に別の人を選びます。名古屋の人だったとしましょう。上と同様に、またその人と十個のボールとの距離を計算します。そうすると九個のボールはまだ鬼界ヶ島にありますが、一個のボー ルはそれよりも名古屋に近い距離にありますので、またこのボールが勝者となり、そのボールと名古屋の距離の 1/10 だけ名古屋寄りに進むことになります。このようにして、一億人から一人を選んで は、その都度ボールとの距離を計算していくと、もし選ばれる人が人口が集中している関西以東の場合は、この一個のボール(代表点)が勝者となってしまいます。しかし、元来、このボール、すなわち代表点は千万人に対して一個割り当てられるはずですので、勝った数が千万人を超えた場合は一旦その距離計算の対象からは外して休憩してもらうことにします。そうすると、それ以外のまだ鬼界ヶ 島に残っているボールの一つが勝者となり本土に近づくことになります。このボールもまた勝つ回数が千万人を超えると休憩してもらいます。 このような勝負を全体の一億人に対して何度も繰り返していきますと、次第に十個のボール全部が人口の少ない鬼界ヶ島を飛び出して日本全国の人口の多い地点を巡り歩くことになります。 当初は勝者のボールが接近する距離は 1/10 でしたが、それを次第に(漸近的に)小さくしていきます。するとついには、全ての十個のボールが大体全国の人口を十等分する点に落ち着く事になります。動きが落ち着いたところで、打ち止めにします。その時この十個のボールのうち、隣あった者同士の距離を折半したところが境界線となります。言い換えますと、この十個のボールの位置はこの境界 線内の領域の重心位置と言えます。 上記のプロセスはまとめると次のようになります。 1.分類したい、代表点を決定する。(上の例では十個) 2.母体のデータから任意のサンプル点を選択する。(上の例では、母体のデータは一億人) 3.複数の代表点と選択されたサンプル点の類似度を計算する。(上の例では地理的距離を測定) 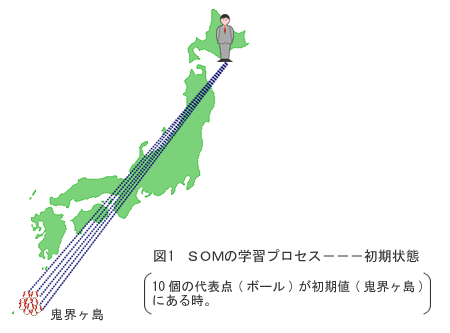
4.一番類似度の高い代表点(これを勝者と名づけました)をサンプル点に少しだけ接近させる。 (上の例では 1/10 だけ接近) 5.特定の代表点が常に勝者とならないように、平均回数(上の例では千万)以上勝った場合は、 暫く休憩する。 6.複数の代表点の変動が落ち着く(収束すると言います)まで2.から5.のプロセスを繰り返す。 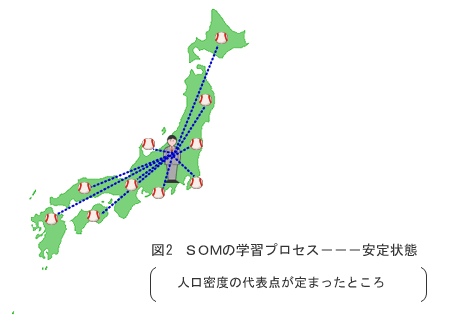
このようなプロセスは手計算ではとてもとても出来ませんが、コン ピュータを使うと、処理自体は至って簡単ですので、非常に早く計算できます。 実際、私もこのSOMのプログラムを作って画面に表示させたことがありますが、見る見る内に代表点が落ち着く(収束する)のを確認することができました。その動きはアメーバーがくねくねと形を変えていくみたいに、自在に変化していきます。接近する距離(上の例では 1/10 )が大きいと代表点がぴょんぴょんととびはねるように見え、逆に小さすぎると、尺取虫のようにじわじわとしか変化しません。このあたりの設定がデータとのからみで難しいところです。 このSOMという手法、原理自体はなかなか簡単ですが、応用範囲の極めて広い手法です。ただ、欠点と言えば、類似度(距離)が計算できないものにはこの方法が適用できませんので、カテゴリーデータ項目(たとえば、職業、男女など)がある場合には適用できません。 また、単位系が必ずしも一致していない場合(例えば、身長、体重、握力)も問題があります。つまり異なる単位系をどのように読み替えるか、という点が問題です。これは以前『データの蜃気楼(その三)』というタイトルで説明しました。『尺度をかえると別のグループに見える』という現象です。SOMを適用する場合でも全く同じ問題が発生します。つまり、単位系を替えるとサンプル点が違ったグループに分類されてしまいます。 従って、分類結果を見て、直感的におかしいと感じたら、単位系の読み替えの設定をおこない直し、再度SOMのプログラムを走らせて下 さい。この意味では、SOMによる分類は恣意的であることを免れることはできません。それはちょうど、始めに述べました例のように、ヒトとチンパンジーのグループ分けで観点を変えると分類結果が変わってしまうのと同様です。 皆さんも一度このSOMを自分達のデータで実際に試されてはいかがでしょうか? |
|
| 続く... |
|
|
△TOPへ Copyright © 2005 Zetta Technology Inc. All rights reserved.
|
|