


|
|
 |
|
| 前回までは、データマイニングでよく使われているニューラルネットワークについて述べてきました。今回は、もう一つのよく使われている手法、Tree分析について述べます。 このTree分析と名前の由来を説明しましょう。Treeとは、樹(木)ですから、Tree分析は日本語では樹形分析とも呼ばれています。 機能的には、前回説明しました、SOM(Self Organizing Map)と似ています。大量データを類似性の観点から、幾つかのグループ(大抵の場合、二分類)に自動的に分類してくれます。SOMと異なり、その分類結果が、ちょうど樹を逆さまに見たようになるところからその名前が付けられています。 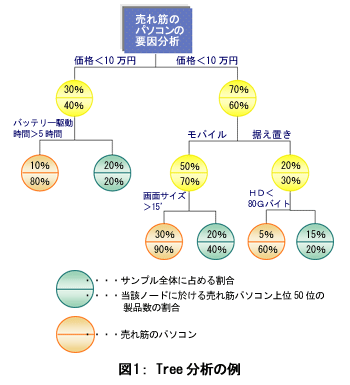
図の一番上の部分、つまり木の根に該当するところに、元のデータが全部あります。そこから、枝が(下方に)伸びていますが、その枝には、まとまりのあるデータが集められます。その時、データ項目のある値(これは枝の上にその条件が記述されています)で右枝と左枝に分かれます。このようにして分かれた枝には、だんだんと類似度の高いデータが集まってくることになります。 このように、Tree分析の原理は至って簡単ですが、分析結果が専門知識のない人達、たとえば営業現場の人達にとっても分かり易いため、いろいろなテーマに応用されています。当然のことながら、利点とは裏腹に欠点もいくつかあります。それは次回説明することに して、今回はTree分析の手法を説明します。 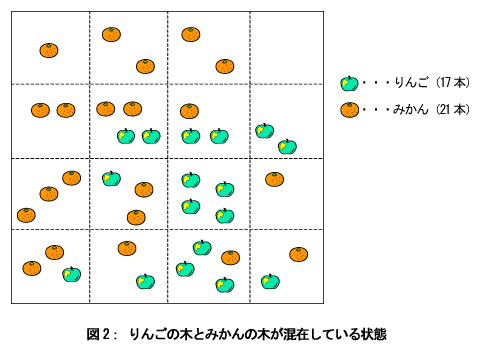 ここに一枚の航空写真があると思ってください。その写真にはリンゴの木とみかんの木混在して植わっている果樹園が写っています。 さて秋になって、リンゴ狩り、あるいはみかん狩りをする地図を作るため、航空写真のなかで、リンゴの木がかたまっている個所(ブロック)とみかんの木がかたまっている個所(ブロック)の印をつけないといけません。 人間だと、ぱっと見て、フリーハンドで線を引いてブロック分割したり(図2-a)あるいは、○を書いてブロック分割したり(図2-b)するでしょう。 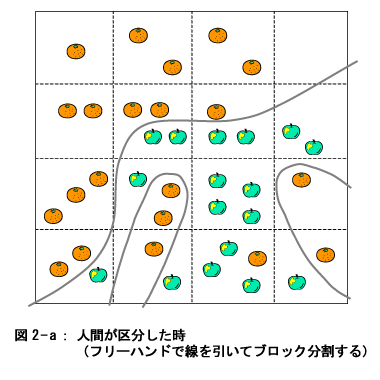
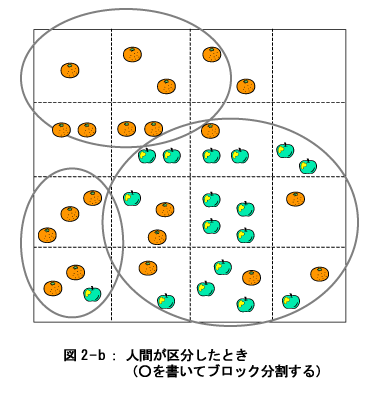 これら分割されたブロックの中には必ずしもリンゴの木、あるいは みかんの木が100%でないこともあります。つまり、リンゴのブロック(つまりリンゴが過半数ある場所)といってもみかんの木も多少混ざっていますし、逆にみかんのブロックにもリンゴの木が幾つか混ざっています。しかし、この別種の混ざり具合(エラー率とも言いますが)がなるべく少なくなるように分割をいろいろ工夫するで しょう。 極端な話、一つのリンゴの木、あるいはみかんの木を一つづつ○で囲ってしまえば、ブロックの分割数は全体の固体数となり、エラー率はゼロとなります。しかし、リンゴ狩する人達にとっては、情報があまりにも繁雑すぎて、リンゴの木がどこにかたまっているのかが分かりづらいことでしょう。このように、情報というのは粗雑でも繁雑でもダメなのです。つまり人間が理解するのに『ちょうどよ い』(つまり、適切な)情報量を越えると反って欲しい情報が得られないということになります。参考までに、この『ちょうどよい』情報量を数学的に求めるのがAIC理論(赤池情報量理論)と呼ばれている理論です。 さて、もとに戻って果樹園のリンゴとみかんの木の領域の塗り分けをコンピュータで自動的に処理するにはどうしたら良いのでしょうか。コンピュータでは、フリーハンドのような任意の線を描くことは得意ではありませんので、直線で分けます。最初からブロックを作ることをせずに、ある一つの軸に並行な直線で大きく二つのブロックに左右(あるいは上下)に分けます。そして、その直線をすこしづつずらしていき、エラー率を求め、最終的にエラー率が最低になるところを見つけます。今回の場合、2次元の平面上での分割ですので、縦と横の二つの軸に並行な直線で分割することになります。 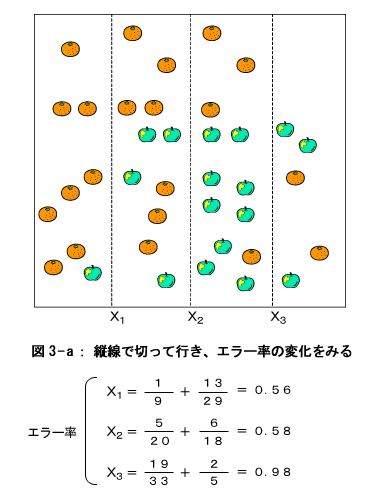 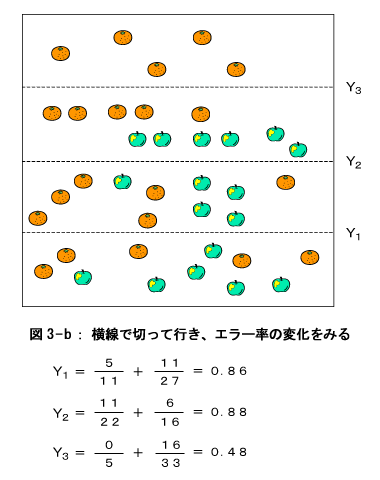
実際には、分割線を連続的(すこしづつ)にずらしていきながらエラー率を計算するのですが、ここでは説明の便宜上、4等分の線で計算することにします。図には、それぞれの分割線におけるエラー率 を計算しています。例えば、図3-aの x1 におけるエラー率は次のようにして求めます。先ず、分割線 x1 の左側にある、リンゴの木とみかんの木の本数を数えます。 リンゴの木=1本 みかんの木=8本 つまり、この部分ではみかんの木の方が多いので、この部分は『みかんの領域』とします。そのように見なすと、1本だけあるリンゴの木は、間違ってみかん領域に存在する、という意味でエラーとな ります。つまりエラー率はこの場合 エラー率=リンゴの木の本数/(リンゴ木+みかんの木)の本数 =1/9 さらに今度は分割のもう一方の領域、つまり x1 の右側の領域についてリンゴの木とみかんの木の本数を数えます。 リンゴの木=16本 みかんの木=13本 この結果、この領域はリンゴの木方が多いですので、リンゴ領域と見なせます。従って エラー率=13/29 結局 x1 で分割したときの総合的なエラー率はこの二つのエラー率を足したものになります。 エラー率=1/9 + 13/29 = 0.56 さて縦横の分割方向で計算したエラー率を比べると、y3の線で切った時が最もエラー率が低い事が分かります。そこで分割の第一段階はこの線で上下に分割し、上部を『みかんの領域』、下部を『仮のリンゴの領域』とします。そしてこの『仮のリンゴの領域』について再度同様の分割を行います。 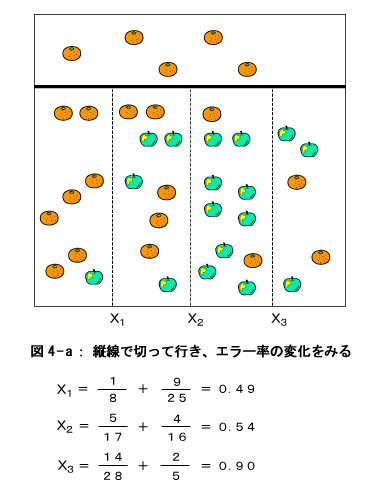
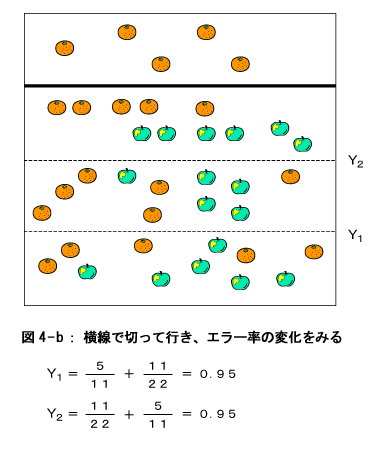 この結果、左端の部分がまたもや『みかんの領域』と決まりました。右の部分も『仮のリンゴの領域』となりました。上のプロセス同様、再度この仮の領域を分割します。 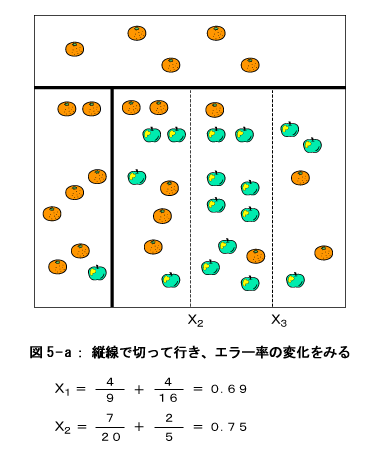
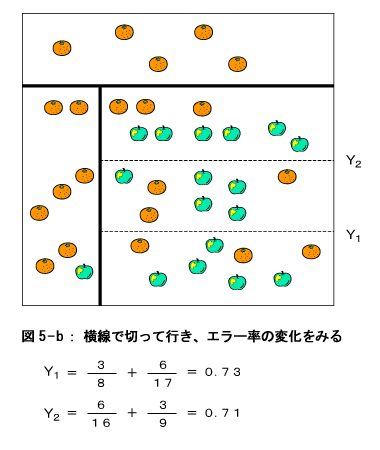
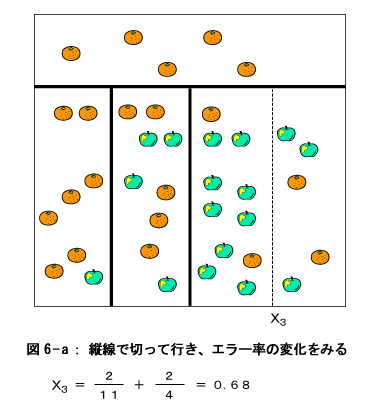 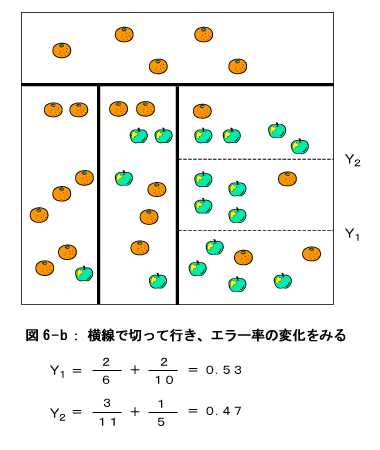
最後に図7のように分割する部分が横線方向しかなくなりました。そして、分割したときとしないときのエラー率を比較しますと、分割しない時の方がエラー率が低いことが分かります。 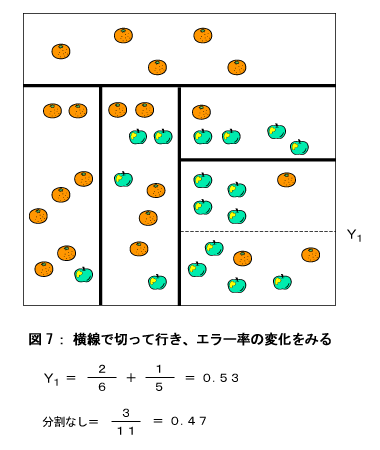
結局、リンゴの木とみかんの木のそれぞれの領域は図8のように決まりました。 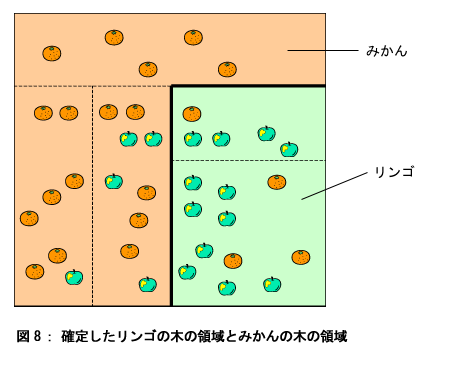
どうですか、Tree分析のしくみ、理解できたでしょうか?このように、Tree分析の計算自体は至って単純で、かつ分析結果も比較的分かり易いため、データマイニングの手法の中ではニューロと並んで最もよく使われています。 |
|
|
続く... |
|
|
△TOPへ Copyright © 2005 Zetta Technology Inc. All rights reserved.
|
|