

【第28回】データマイニング・夜話
(その十:子供の頃わくわくした事)
コラムTOPへ戻る

|
|
 |
|
【第28回】データマイニング・夜話 (その十:子供の頃わくわくした事) コラムTOPへ戻る |
|
| 『少年よ大志をいだけ』という言葉は言うまでもなく、クラーク博士(William Clark )の言葉です。クラークは明治初年(1876年)日本政府から札幌農学校(後の北海道大学)に招聘されましたが、滞日はわずか1年です。しかし、彼の残した言葉は若者だけでなく日本人全体に広く知られて、常にみずみずしい感動を与えています。 中国の故事成語のこれに匹敵する言葉として『鶏口となるも、むしろ牛後になるなかれ』が挙げられます。今から2400年前、中国が群雄割拠していた時、蘇秦(そしん)という国際政治コンサルタントが韓という弱国に他の弱国と連携して強国の秦に対抗させるための説得の一場面に使った言葉です。『一人前の独立国である韓が、何もわざわざ、卑屈にも秦にへりくだる必要はないではありませんか !世間でも鶏の頭でいる方が、牛の尻尾であるよりましだと言っているではありませんか!』とアジテートした訳です。 世間知らずの韓王(宣恵王)は蘇秦の思いどおり弱小国連合に加盟することになります。しかし、結局歴史の歯車は蘇秦の思う方向とは逆に六国は続々と秦に征服され、遂に紀元前221年、始皇帝の全国統一となるわけです。 さて、この蘇秦が活躍していた当時(今から2400年ほど前)の中国の各地の都は大変混雑していたようです。斉(山東省)の都の兵士の数は『三七、ニ十一万』と言っています。つまり、一家に成年男 子が三人、戸数が七万戸があるから、掛け算して合計で21万人、という次第です。これから類推すると、斉の都の人口は50万人ぐらいと考えられます。その混雑ぶりは、次のように表現されています。『歩いている人の着物の襟や袖がまるで、カーテンのように街路を覆っている。人の汗がしたたり落ちるのはまるで雨が降っているようだ。』(連衽成帷、挙袂成幕、揮汗成雨)中国人は、何かにつけ『白髪三千丈』式に大げさに言いますが、この場合もかなり割り引いて聞いておく必要がありそうですね。ちなみに、『白髪三千丈』とは、李白が『私の髪の毛は憂いのために白くなって、6キロメートルにもなってしまった』(白髪三千丈、縁愁似個長)と嘆いた詩から来ています。 このような誇張は、人を説得する時に使うレトリック(話術)の一つですが、さらに意表をつく言い回しもあります。例えば世の中には悪人は多いものの、極め付きの善人(つまりマザーテレサのような聖人)は少ないと慨嘆した言い方として、『聖人というのは、千年に一度出現しても、踵(きびす)を接している』(累世而有一聖人、継踵也)があります。通常『踵(きびす)を接す』という言葉は、雑踏のなか、前の人の踵(かかと)に後の人のつま先がぶつかってしまう場合に使います。千年に一度の出現では、とてもそのような込み合っている状態ではないですが、本来聖人が世の中に現れるのがまれであるので、千年に一度でもひしめく程多いというのがその理屈です。 さて、このようなレトリックはさておき、まれに起こる現象を数学的にモデル化したのがフランスの数学者、ポワソン(Poisson、1781 - 1840)です。それは通常、ポワソン分布(Poisson distribution)と呼ばれています。 この式が最初に適用された事例としては、プロシャ陸軍の兵士が馬に蹴られて死亡する事故のデータ分析が有名です。1875年から1894年までの計20年間に馬に蹴られて死亡した兵士の数を200部隊に対して調べたところ以下のような結果を得られたそうです。 死亡者数 部隊数 0人 109 1人 65 2人 22 3人 3 4人 1 計 200 簡単な計算によって、これらの数字から各部隊の平均死亡者数は 0.61人となることが分かります。 さて、この値を理論値と比較してみましょう。 ポワソン分布の式は次式で与えられますので、これを計算してみましょう。 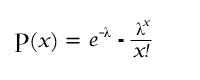 プロシャ兵が馬に蹴られて死亡する率(理論値と実際値)
この2つのコラムを比較しますと、ポアソン分布の理論値は実際値によくあてはまることがわかります。 もう一つの例として、ある都市の交通事故の発生確率を考えて見ましょう。交通事故はそれほど頻繁に発生しませんのでポワソン分布が使えそうです。都市の人口を10万人、交通事故が一日平均で6件発生する場合を考えましょう。 このような場合、ポワソン分布を計算すると正規分布に非常に近い値が得られます。それを検証してみましょう。 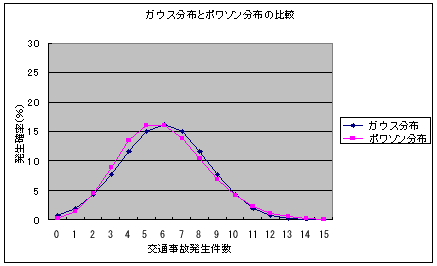 この図から分かりますようにポワソン分布とガウス分布はこのようなケースでは、実質的には差がない、つまり、ポワソン分布はガウス分布で近似できることが分かります。 さて、交通事故というのは日によって多く発生したりほとんど発生しなかったりしますが、どの程度であれば、異様に(少ない/多い)と言えるかを考えてみましょう。 このようなケースを検討する場合、検定という理論を使います。検定にはいろいろな種類があります。代表的なものは: t 検定、F 検定、Wilcoxon(ウィルコクスン)検定 があります。 2つの分布の場合、例えば、中学校の2クラス(クラスAとクラスB)の英語のテストの点数の分布を考えて見ましょう。 t 検定 -- 2つのクラスの平均値が等しいとみなして差し支えないかを検定し(確かめ)ます。 F 検定 -- 2つのクラスの点数のばらつき(標準偏差)が等しいとみなして差し支えないかを検定し (確かめ)ます。 さて、t 検定も F 検定もどちらもデータの分布が正規分布であることを(暗黙の内に)想定しています。しかし、データによっては必ずしもその前提が適応できないケースもあります。そのようなときは分布の形状ではなく、単に順位だけで確認する方法もあります。それをノン・パラメトリック検定と呼んでいます。その代表的なものがWilcoxon(ウィルコクスン)検定と呼ばれています。 Wilcoxon検定 -- まず、2つのクラスの成績順位をつけます。そして2つのクラス合同の総合順位 をつけます。そして各クラスの総合順位の合計を別々に計算します。互いの総 合点が等しいとみなして差し支えないかを検定し(確かめ)ます。 このように検定の手法自体は検定する対象データ、あるいは検定目的に応じてさまざまですが、基本的には次の考え方です。 『同じというのは、値(平均値や分散)が完全に一致する必要はない。ただ、それが許容範囲にあるかどうかである。許容範囲とは、普通の状況で95%の確率で起こる範囲である。』と考えています。つまり100回のうち5回ぐらいはその範囲より外れても許せると見なしている訳です。 その検定の概念を使って、今回の交通事故の発生確率の場合を検討してみましょう。つまり、10万人都市では、1日平均6件の交通事故があるとした場合、何件ぐらい発生すれば、異様に(少ない/多い)といえるのでしょうか?それには、上記のポワソン分布の発生確率の累積数を計算する必要があります。 交通事故発生確率
交通事故の少ない方では、累積%が5%の点を見ますと、2件未満ですから、1日あたり1件以下しか起きなければ、その日は交通事故が異様に少ない日であるといえます。逆に、累積が95%の点を見ますと10件ですので、1日あたり、10件以上発生すると、その日は交通事故が異様に多い日であるといえます。 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
続く... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
△TOPへ Copyright © 2006 Zetta Technology Inc. All rights reserved.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||