

【第28回】データマイニング・夜話
(その十:子供の頃わくわくした事)
コラムTOPへ戻る

|
|
 |
|
【第28回】データマイニング・夜話 (その十:子供の頃わくわくした事) コラムTOPへ戻る |
|
| 私たちが普段なにげなく使っている単語の中には、随分と古くから使われている単語があります。『臍(ほぞ)を噬(か)む』という単語は2500年以上も前の中国の歴史書『春秋左史伝』に載っています。一説には、猟師がしかけた罠にかかって、もがいていた鹿を罠からはずそうとしたら、鹿がしきりに臍(へそ)の辺りを噛もうしたらしいのです。その様子があたかも罠にかかったのを悔やんでいるらしく見えたので、『臍を噬(か)む』という動作が『反省する』という意味に用いられるようになったと言われています。 元来とは違った意味にとられて使われた単語に、『挙燭(燭を挙げよ)』と言うのがあります。ある地方の役人が夜中に中央官庁の大臣へ手紙を書いていました。手元が暗かったので、提灯持ちに『ライトを持ち上げよ(挙燭)』と命令しましたが、言うだけでなく、ついでに手紙にもそう書いてしまったのです。その手紙を受け取った大臣は、この文句の意味が分からず暫く考えていました。その内にこれは、『ライトというのは賢人のことだ。つまり、賢人を採用しろ、という意味に違いない』と考え、実行しました。その結果当地の政治はうまく治まったということです。 このような故事成語は中国には数多くありますが中でも論語は人口に膾炙している言葉の宝庫です。『過ぎたるはなお及ばざるが如し(やりすぎは害になる)』というのもその一つでしょう。 私の経験からこの言葉がぴったりと当てはまる例を紹介しましょう。以前あるクレジットカード会社にデータマイニングのコンサルティングをしていた時のことでした。そこの部長さんから、ある晩相談に乗ってくれと電話がありました。話を聞いてみると、同社では、データ解析にエントロピーをベースにしたTree(樹形)分析ソフトを使って、カード保有者の動態スコアリングモデル(Behavior Scoring)を作成していました。悩みというのは、モデル作成の時は素晴らしく高い(良客/不良客)判別性能(90%以上)が出るのに、いざ、実際に運用してみると、全くぼろぼろになるらしいのです。 私はそれを聞いていて、まさに『過ぎたるはなお及ばざるが如し』だな、と思いました。つまり、Tree(樹形)分析というのは、以前(第10回)説明しましたように、細かく分析すればするほど精度は上がるのですが、実は一般的な傾向を把握する観点からは逆にどんどんと離れていってしまうのです。 どの辺りで分析をストップするかについては、客観的なルールがありませんので、下手をするとこの部長さんのように大怪我をすることになりかねません。 今回は、エントロピーをベースにしたTree(樹形)分析の仕組みを説明します。 次のような例を考えて下さい。ここに8人がいます。酒の好みを聞いたところ、日本酒派と洋酒派に分かれました。それぞれには3つの属性があります。 性別={男,女} 出身地={札幌,神戸,長崎} タバコを吸うか?={吸う,吸わない} さてここで質問ですが、日本酒派と洋酒派に分けるにはどの属性に注目するのがいいでしょう。この方法を考えてみましょう。 A 日本酒 {男}{札幌}{吸う} B 洋酒 {男}{神戸}{吸う} C 日本酒 {女}{長崎}{吸わない} D 日本酒 {女}{札幌}{吸う} E 日本酒 {男}{長崎}{吸わない} F 日本酒 {男}{札幌}{吸わない} G 洋酒 {男}{長崎}{吸う} H 洋酒 {女}{長崎}{吸う} 【現状調査】 まず、現状(未分割時)のエントロピーを計算します。 8人のうち、洋酒を飲むのが3人、日本酒を飲むのが5人。つまり、洋酒の割合が (3/8)、日本酒の割合が(5/8)となります。 これらの値から情報エントロピーを計算しましょう。情報エントロピーは前回の話から次の式で与えられましたね。 エントロピー = - sum [ p * log(p) ] 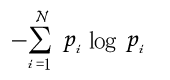 これから 現状のエントロピー = -(3/8) * log(3/8) - (5/8) * log(5/8) = (-0.375) * (-1.415) + (-0.625) * (-0.678) = 0.531 + 0.424 = 0.954 【グループ分割をする】 次に、この8人をいろいろな属性で分割することで、まとまりのあるグループを作れるか検討しましょう。 それにはいろいろの分け方があります。 その1:男女で分ける その2:出身地で分ける その3:タバコを吸うか/吸わない、で分ける 【その1:男女で分ける】 【男】 A 日本酒 {男}{札幌}{吸う} B 洋酒 {男}{神戸}{吸う} E 日本酒 {男}{長崎}{吸わない} F 日本酒 {男}{札幌}{吸わない} G 洋酒 {男}{長崎}{吸う} 【女】 C 日本酒 {女}{長崎}{吸わない} D 日本酒 {女}{札幌}{吸う} H 洋酒 {女}{長崎}{吸う} この時のエントロピーを計算してみましょう。 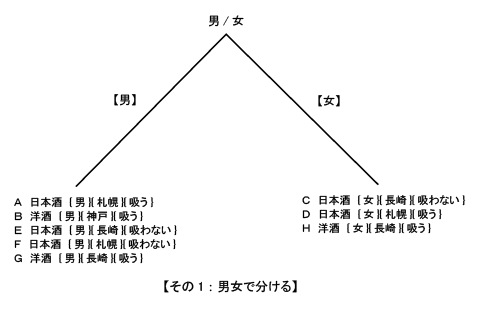 男のエントロピーは: 5人のうち、洋酒を飲むのが2人、日本酒を飲むのが3人。 つまり、洋酒の割合が (2/5)、日本酒の割合が(3/5)となります。 これらの値を上記の情報エントロピーの式に代入すると 男のエントロピー = -(2/5) * log(2/5) - (3/5) * log(3/5) = (-0.4) * (-1.322) + (-0.6) * (-0.737) = 0.529 + 0.442 = 0.971 同様にして、女のエントロピー = -(1/3) * log(1/3) - (2/3) * log(2/3) = (-0.333) * (-1.585) + (-0.666) * (-0.585) = 0.528 + 0.390 = 0.918 このわけ方、つまり男女で分けた場合のエントロピーは男が5人、女が3人ですので、結局次のようになります。 男女に分割した時のエントロピー = (5/8) * (男のエントロピー) + (3/8) * (女のエントロピー) = 0.625 * 0.971 + 0.375 * 0.918 = 0.607 + 0.344 = 0.951 【分割結果--男女】 男女で分割したときのエントロピーは元の値と比較すると: 差分 = 0.954 - 0.951 = 0.003 だけ低下しています。つまり、分割したことで日本酒派と洋酒派の まとまり具合がわずかながら向上したのです。 【その2:出身地で分ける】 同様にして出身地で分けてみましょう。 札幌 A 日本酒 {男}{札幌}{吸う} D 日本酒 {女}{札幌}{吸う} F 日本酒 {男}{札幌}{吸わない} 神戸 B 洋酒 {男}{神戸}{吸う} 長崎 C 日本酒 {女}{長崎}{吸わない} E 日本酒 {男}{長崎}{吸わない} G 洋酒 {男}{長崎}{吸う} H 洋酒 {女}{長崎}{吸う} この時のエントロピーを計算してみましょう。 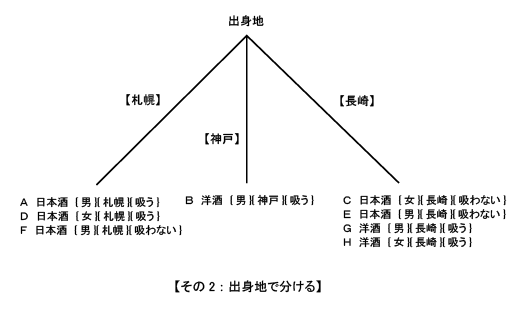 札幌のエントロピーは: 3人のうち、日本酒を飲むのが3人(全員)です。 札幌のエントロピーは = -(3/3) * log(3/3) = -1 * 0 = 0 同様に神戸のエントロピーは: 1人のうち、洋酒を飲むのが1人(全員)です。 神戸のエントロピーは = -(1/1) * log(1/1) = -1 * 0 = 0 長崎のエントロピーは: 4人のうち、洋酒を飲むのが2人、日本酒を飲むのが2人です。 長崎のエントロピーは = -(2/4) * log(2/4) - (2/4) * log(2/4) = (-0.5) * (-1.0) + (-0.5) * (-1.0) = 0.5 + 0.5 = 1.0 このわけ方、つまり出身地分けた場合のエントロピーは札幌が3人、神戸が1人、長崎が4人ですので、結局次のようになります。 出身地で分割した時のエントロピー = (3/8) * (札幌のエントロピー) + (1/8) * (神戸のエントロピー) + (4/8) * (長崎のエントロピー) = (3/8) * 0 + (1/8) * 0 + 0.5 * 1.0 = 0.5 【分割結果--出身地】 出身地で分割したときのエントロピーは元の値と比較すると: 差分 = 0.954 - 0.5 = 0.454 だけ低下しています。つまり、分割したことで日本酒派と洋酒派のまとまり具合がかなり向上したことが分かります。 【その3:タバコを吸うか/吸わない】 吸う A 日本酒 {男}{札幌}{吸う} B 洋酒 {男}{神戸}{吸う} D 日本酒 {女}{札幌}{吸う} G 洋酒 {男}{長崎}{吸う} H 洋酒 {女}{長崎}{吸う} 吸わない C 日本酒 {女}{長崎}{吸わない} E 日本酒 {男}{長崎}{吸わない} F 日本酒 {男}{札幌}{吸わない} この時のエントロピーを計算してみましょう。 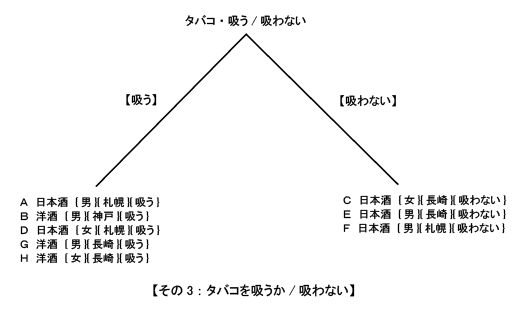 吸うのエントロピーは: 5人のうち、洋酒を飲むのが3人、日本酒を飲むのが2人です。 吸うのエントロピー = -(3/5) * log(3/5) - (2/5) * log(2/5) = (-0.6) * (-0.737) + (-0.4) * (-1.322) = 0.442 + 0.529 = 0.971 吸わないのエントロピーは: 3人のうち、日本酒を飲むのが3人(全員)です。 吸わないエントロピー = -(3/3) * log(3/3) = (-1.0) * 0 = 0 このわけ方、つまりタバコを吸う/吸わないで分けた場合のエントロピーは吸うが5人、吸わないが3人ですので、結局次のようになります。 吸う/吸わないで分割した時のエントロピー = (5/8) * (吸うのエントロピー) + (3/8) * (吸わないのエントロピー) = (5/8) * 0.971 + (3/8) * 0 = 0.607 【分割結果--吸う/吸わない】 タバコを吸う/吸わないで分割したときのエントロピーは元の値と 比較すると: 差分 = 0.954 - 0.607 = 0.347 だけ低下しています。 【結論】 以上の分析をまとめると次のようになります。 A.分割前のエントロピー = 0.954 B.分割後のエントロピー これらの分割の内、エントロピーが一番低いのが出身地で分割した時です。つまり、この与えられたデータからいうと、出身地でその飲む酒の種類が分かるとかなり正しく判断できるということです。 D.過ぎたるはなお及ばざるが如し このような分析はまだまだ続けることができます。しかしエントロピーが下がる(つまり分析精度が上がる)からといって、むやみに細かい分割をしないように注意しましょう。どこで分割を止めるか、については残念ながら一般的ルールはありません。分析モデルを何回か実際に使ってころあいを会得するようにしてください。 ちなみに 出身地の{札幌,神戸,長崎} は私がカラオケで自信をもって歌える数少ない持ち歌、『中ノ島ブルース』に出てくる街でした。 |
|
|
続く... |
|
|
△TOPへ Copyright © 2006 Zetta Technology Inc. All rights reserved.
|
|