

【第28回】データマイニング・夜話
(その十:子供の頃わくわくした事)
コラムTOPへ戻る

|
|
 |
|
【第28回】データマイニング・夜話 (その十:子供の頃わくわくした事) コラムTOPへ戻る |
|
| 前回は『併時発生頻度による類似度マトリックスを使った概念的データモデリング法』、通称McSim(マクシム)の応用分野について述べました。今回はちょっと難しくなりますが、深堀をしてその技術的な側面を述べてみましょう。 ここで述べる方法は、McSimに特有ではなく、ニューラルネットワーク(ニューロ)に共通の考え方です。つまりニューロというのは、以前も述べましたが(第7回参照)数学的観点からいうと、『非線形の最適化技法』です。 これらの技法に共通な特徴は、次の手順を必ず踏むことです(第8回参照)。 【ニューロの学習則】 1. 初期パラメータ値を決める。 2. その時のパラメータ値から計算式(評価関数)の値を計算する。 3. 計算式の値が良くなるようにパラメータ値を少しだけ変化させる。 4. 計算式の値が良くなるまで2.と3.のプロセスを繰り返す。 5. 計算式の値があまり変化がなくなったら、終了する。 実社会でこのプロセスの喩えますと 学校を卒業して就職を探している若者がいたとしましょう。なるべく多く給料をもらいたいと思っています。しかし、どのような業種・業態の会社の給料が高いのかを知りません。またどのような資格をとると給料が上るかも知りません。このような条件でどのようにしたら、高い給料をとることができるでしょうか?上の手順をたどってみましょう。彼がとる行動は次のように手順化できます。 【高給取りになる学習則】 1. 適当にどこかの会社に入る。当然のことながら、入った会社が必ずしも世間で一番高い給料の 会社とは限りません。 2. もらった給料の計算をする。 3. 何らかの資格をとる。同時に他社の同世代の給料を聞く。 4. 取った資格で給料が上がるなら(2.の計算の結果)、それに類した資格をどしどし取る。 あるいは、他社の給料が高いのなら、会社を変わる。 5. その内にたくさんの資格を持つようになり、それ以上いくら資格をとっても給料が変わらないよう になる。(大抵は管理職になると資格のあるなしではあまり給料自体は変わらないもの。) また会社を変わってもあまり給料が上がらなくなる。つまり、自分の年代では最高に近い給料を もらっていることになります。こうなったら、いわゆるさいころの上がり目ですから、もうそれ以上 資格もとらず、また転職もしないでずっと今の所に居続けることになります。 これでニューロのやり方が理解できたでしょうか?ニューロというのはこういったことを内部で何回となく計算しているのです。 さてMcSimで注目しているのは『併時発生』(Mutual Cooccurrence)という現象です。前回挙げた例ではビールとするめが同時に買い物かごの内に入っているという事象(現象)は、スーパーでは頻繁 に見られます。これが併時発生といわれます。つまり、併時発生が頻繁な品目はたとえ全く異なるカテゴリーのアイテム(商品)であっても、意味的には近いカテゴリーであると考えるわけです。 類似度マトリックス(Similarity Matrix)この併時発生の頻度をベースとして、各アイテム(商品)の類似度を各々ペアー(対)で求めましょう。類似度は、+1(完全に類似)〜0(無関係)の連続値で表現することにします。これをマトリックス(表)表示すると、次表の様に対角線上は必ず1となり、それ以外は類似しているもの程1に近い値となります。全く併時発生しなかったもの(例:ビールとローレックス)は0となるという点に異存はないでしょう。 表1:類似度マトリックス 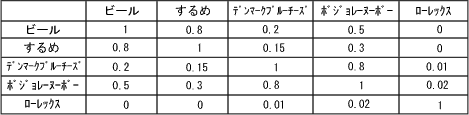 さて、この類似度マトリックスを表現する手段として、多次元ベクトル室間を用いることにします。イメージ的には、地球儀のような球体を考え、その表面に点をとり、球の中心と結ぶベクトル(線分)を考えてください。 図1:類似度マトリックスのベクトル表現例 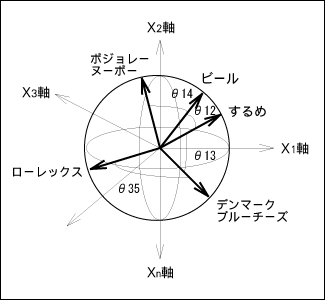 さて、ここで問題というのは、商品ごとの併時発生の頻度をどのようにしてこのベクトル表示に変換できるかという点です。以下にその概略をPOSデータのバスケット分析の例を使って示します。 【ステップ1】 まず、顧客単位の購入データを集計します。各アイテム(商品)の発生(購入)頻度と併時発生(他のアイテムとの組合せが発生)頻度をカウントします。 表2:発生頻度、および併時発生頻度のカウント  【ステップ2】 POSのデータなどでは、商品アイテムが数万、あるいは数十万にもなります。しかし、8・2の法則(売り上げの8割は、2割の商品アイテムで達成されている)を適用すると、すべての商品アイテムを考える必要はなく、発生頻度(単独及び併時)の高いものを考えるだけで十分であることがわかります。この法則を適用して、発生頻度の高い商品アイテムの上位のアイテムだけを抽出します。 【ステップ3】 これらの選択されたアイテム間だけの発生頻度を再度全データからカウントしなおします。 表3:併時発生頻度の上位だけを抽出した表 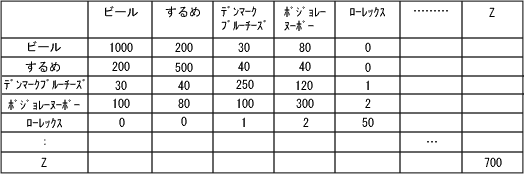 【ステップ4】 この併時発生頻度表を見ますと、対角線上にはその商品の全数が記載されています。また対角線をはさんだ数字は対称となっています。それで、この対角の数字でそれぞれの縦の数値、および横の数値を割ります(正規化する)と、対角線上は1となり、それ以外の場所の値は、必ず0から1の間にある値となります。これが、類似度マトリックスと呼んでいたものです。 表4:類似度マトリックス  【ステップ5】 ここまでで、ようやく問題の本質が明らかになりました。つまり、類似マトリックスの値を図1のようなベクトル表現で表せるか?ということに帰着します。 いろいろな手法が考えられるでしょう。たとえば、図のベクトル間の内積が、類似マトリックスの値となるとすれば、それは一つの解答となります。 しかし、元来複数のベクトル同士がどのような配置にあれば、この類似マトリックスの表の値になるかという点に関しては解析的に完全に求めることはできません。しかし、実はこのような問題こそが ニューロ的に解くのに適しているのです。 上に述べた【ニューロの学習則】を思い出してください。そうすると次のような至って簡単な方法が見つかります。 【類似マトリックスの値の求め方】 つまり、初めは、それぞれの商品アイテムのベクトルに適当な値を与えます(初期配置)。 そして、それぞれの商品アイテムのベクトル同士の内積を計算して、本来の値(類似マトリックスの値)との誤差が少なくなるように、互いのベクトルを少しだけ移動させます。 このようにしてデータ全体を繰り返し学習することで徐々に初期誤差が相対的に小さくなっていきます。 【結論】 今回はかなり技術的に難しい点が多かったですが、理解いただけたでしょうか? 技術的に深堀りした書き方をしたのは、ニューロというのは、決まりきった方法をさす名称ではなく、データ構造を解析するための基礎的な考え方だということを説明したかったからです。 出だしは、適当でも、徐々に修正していくことで、最終的に求める解に到達できるのです。それは、粘土を使って像を作るようなものとも言えるでしょう。初めに大体の輪郭を作ってから、粘土を付け加えたり取り除いたりして、徐々に最終的な形に成形していくプロセスなのです。 データ解析と言えば味気ない、決まりきった手順のみを踏めばよいのだ、という考え方がどうやら世間には蔓延している様ですがニューロの世界を知るとそれらの考え方が単なる因習に過ぎなかったのだ、と目が開かれる思いがすることでしょう。 |
|
|
続く... |
|
|
△TOPへ Copyright © 2005 Zetta Technology Inc. All rights reserved.
|
|